Radial Basis Function Interpolation

Radial Basis Function Interpolation (RBF Interpolation) is a method used to estimate values at unknown locations based on known (source) data points. It works by finding a smooth surface that passes through or near the known points, using a mathematical formula called a “radial basis function” to determine how much each known point influences the unknown locations.

It is like connecting the dots on a map but in a way that creates a smooth, realistic surface rather than straight lines. RBF interpolation is particularly useful when the data points are scattered unevenly across a region, such as measurements taken at irregular locations.

For example, RBF Interpolation can create a smooth geochemical map that fills in the gaps between spare geochemical measurements on rock samples across a large region, making it easier to see trends like positive or negative anomalies.

Interface

The parameters controlling the RBF Interpolation are shown in the figure below.

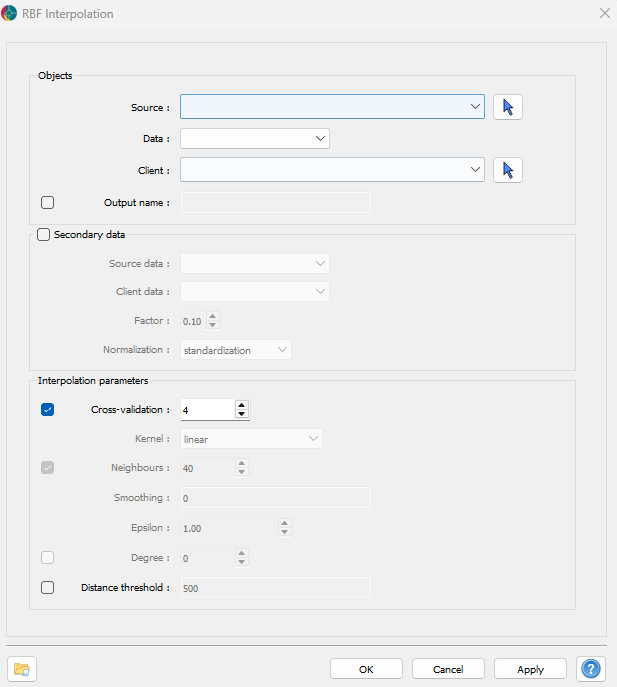
• Source: The object containing the data to use for the interpolation.

• Data: The primary data to interpolate.

• Client: The object on which the data will be interpolated.

• Output Name (optional): The name of the output object. If not specified, the name will default to “The name of Data” + “RBF_interpolated.”

Secondary Data (optional)

If activated, users can include secondary data for the interpolation. The following options are available:

• Source Data: The secondary data from the source object.

• Client Data: The secondary data from the client object.

• Factor: A factor assigned to the secondary data to weight its influence on the interpolation.

• Normalization: The normalization method for the secondary data. Options include:

  • Standardization: Normalize to zero mean and unit variance.

  • Min-Max: Scale values to a range between 0 and 1.

  • Quantile: Normalize data based on its quantile distribution.

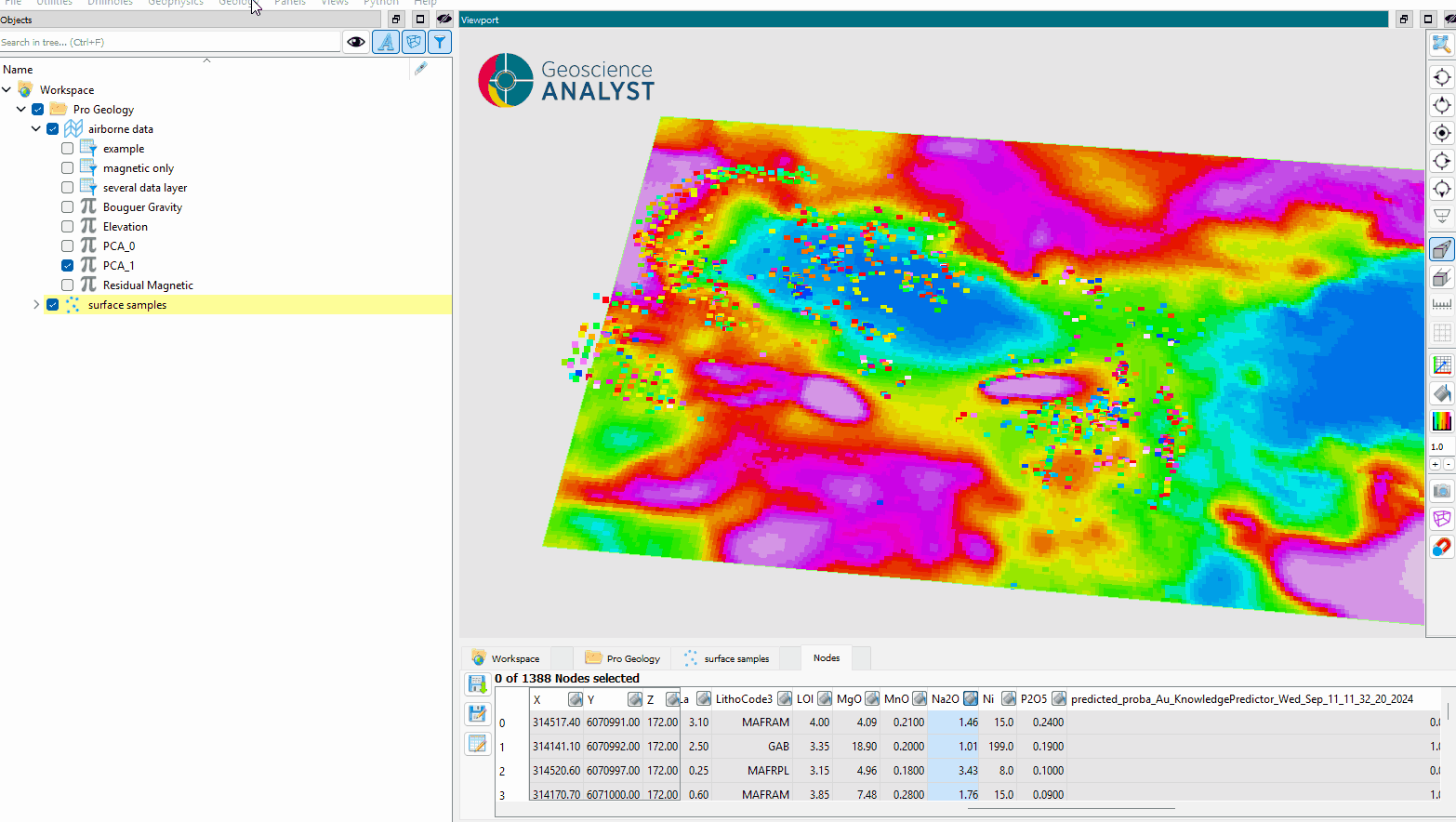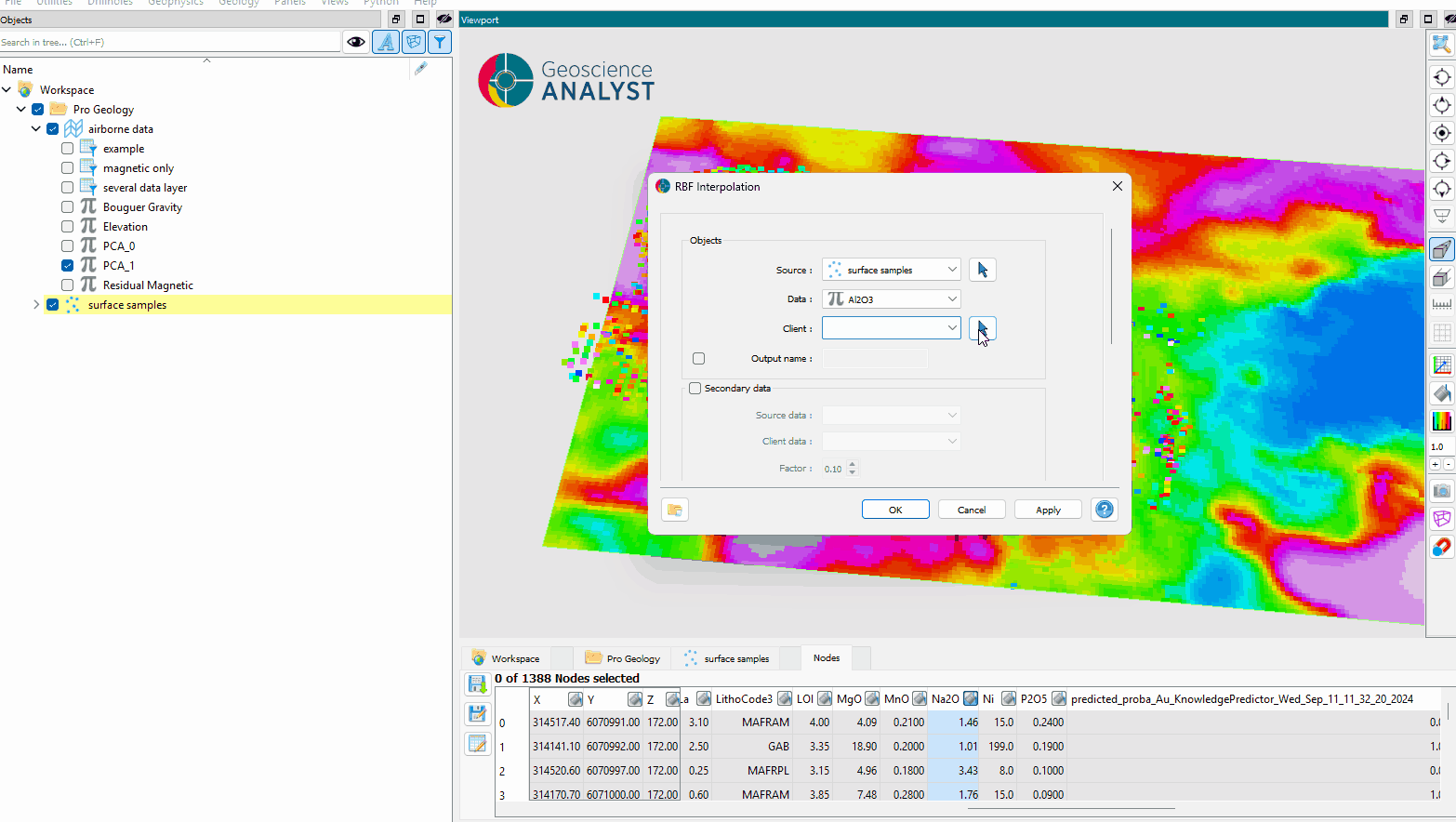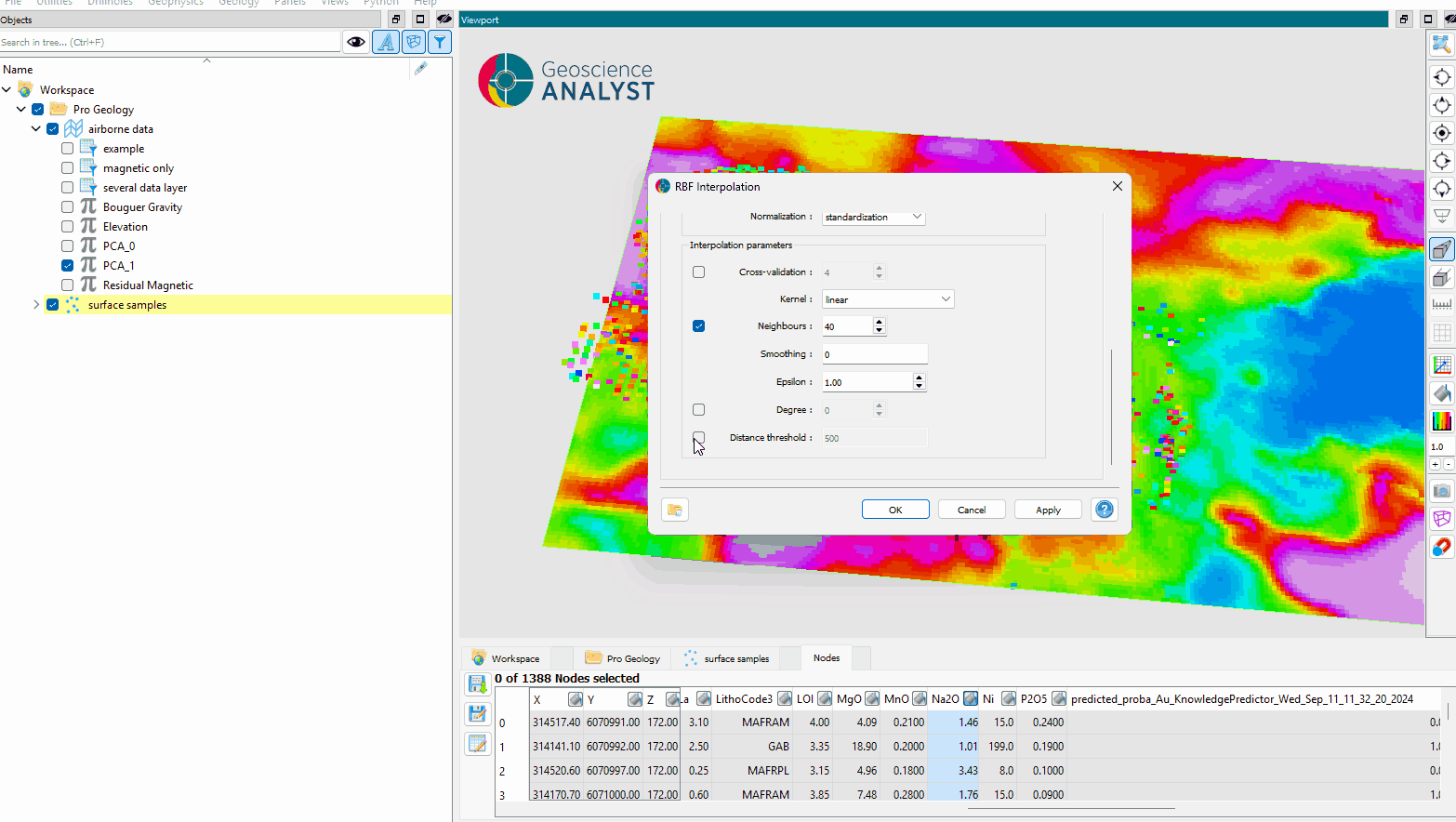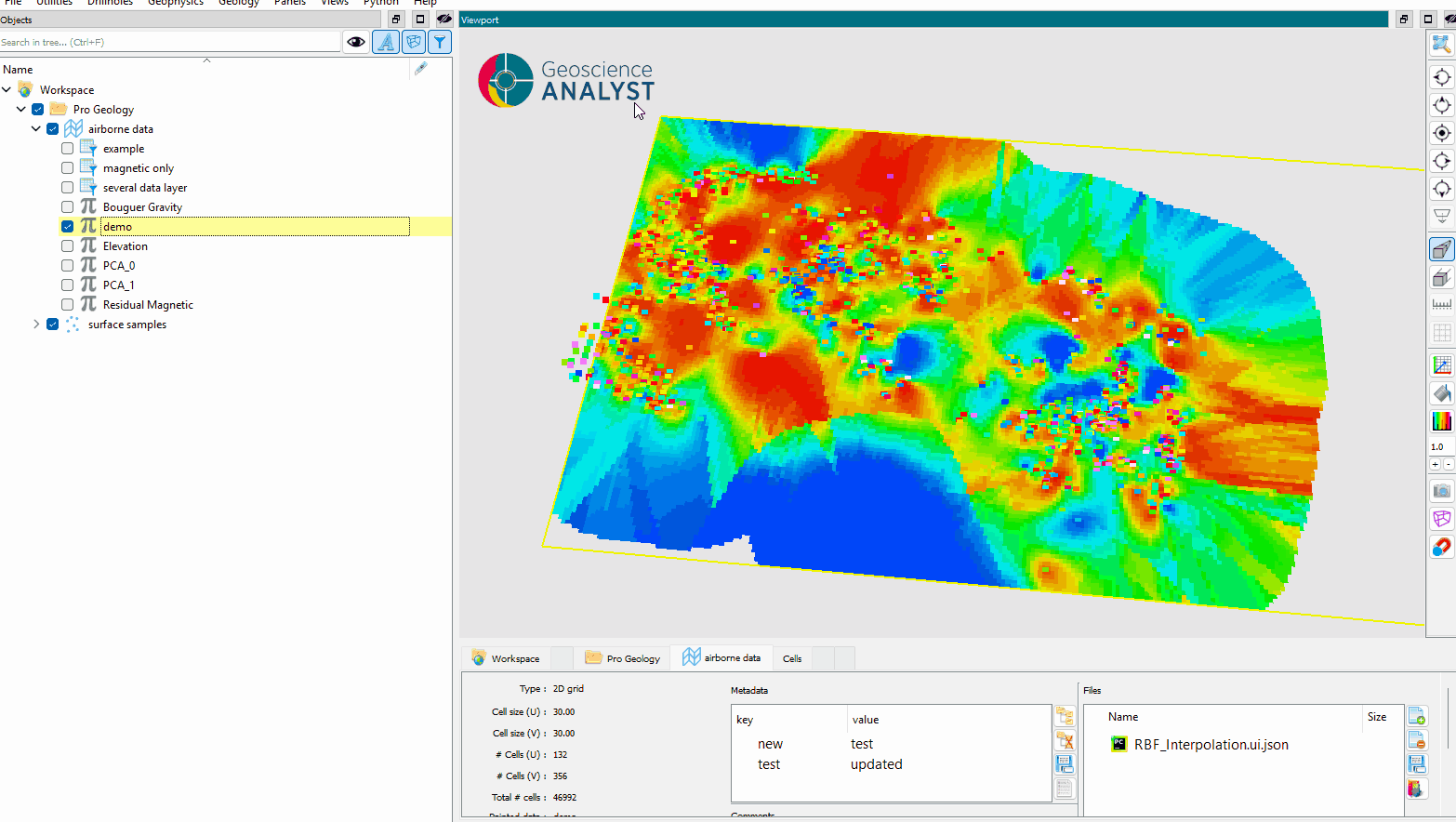
Interpolation parameters

The interpolation parameters, such as Kernel, Neighbours, Smoothing, Epsilon, and Degree, are defined in the scipy.interpolate.Rbf documentation. Refer to this documentation for detailed descriptions and usage guidelines.

• Cross Validation: If activated, optimal parameters will be determined using cross-validation. Users can specify the number of cross-validation groups. If not activated, users can manually set the RBF interpolation parameters.

• Kernel: The kernel determines the mathematical function used to calculate the influence of each known data point on the unknown points being interpolated. Different kernels (e.g., Gaussian, Multiquadric) produce different shapes of influence, which can affect how smoothly or sharply the interpolation behaves.

• Neighbours: This parameter specifies the number of nearby data points considered when estimating the value at an unknown location. Using fewer neighbors can make the interpolation faster but may lose detail, while using more neighbors may capture more spatial trends at the cost of increased computation.

• Smoothing: Smoothing controls the trade-off between perfectly matching the known data points and creating a smoother, more general surface. A smaller smoothing value fits the data exactly but may overfit, while a larger value produces a smoother result that might ignore minor variations in the data.

• Epsilon: Epsilon determines how wide or narrow the influence of each source point is, effectively shaping the “reach” of each point in the interpolation. A small epsilon makes each point influence only its immediate surroundings, while a larger epsilon spreads the influence over a wider area.

• Degree: This parameter specifies the complexity of the polynomial used in the interpolation. A higher degree can model more complex surfaces but may lead to overfitting, while a lower degree creates simpler, more generalized surfaces.

• Distance Threshold (optional): If activated, only points within the specified distance to source points will be interpolated.

Pre-processing

The following pre-processing steps are performed by the function before applying the interpolation:

• Filtering Points:

  • Only points containing valid values are kept for interpolation.

  • In the case of secondary variables, all points containing “no-data” values will be excluded.

• Coordinate Normalization:

  • The coordinates are centered by subtracting their mean and divided by a local variance.

  • The local variance is calculated as the mean of the local variances within a radius defined by a percentage of the largest diagonal of the dataset, defined by the Factor parameter.

• Secondary Variable Normalization:

  • Secondary variables are normalized by a method defined by the user.

• Normalization of the Primary Data:

  • The data to be interpolated is normalized by subtracting its mean and dividing by its standard deviation.

  • After interpolation, the results are transformed back to the original scale by multiplying by the variance and adding the mean.

• Distance-Based Filtering (optional):

  • If activated, data further than a specified distance from the points to interpolate will not be interpolated.

Warning

The RBF function depends on the range of the input data, so proper normalization is crucial for accurate results.

Tutorial

The following video presents a tutorial on how to use the RBF Interpolation application.

• Select the object containing the data to interpolate.

• Select the data to be interpolated.

• Select the object to project the interpolated data onto.

• (Optional) Define the name of the output object.

• (Optional) Select the secondary data for the source object.

• (Optional) Select the secondary data for the client object.

• (Optional) Define a distance threshold to limit the interpolation range.

• Run the application.

• Inspect the results.