Principal Component Analysis

Principal Component Analysis (PCA) is a dimensionality reduction technique that simplifies complex datasets by identifying principal components—directions of maximum variance in the data. These components are linear combinations of the original properties, ranked by their importance in explaining the variance.

For example, PCA can highlight geochemical trends from core samples in magmatic settings. A principal component with high silica can indicate samples of granitic compositions, while another component rich in iron may indicate magma mixing. Various components combined can help geologists identify magmatic processes or compositional patterns.

Pre-processing

Before proceeding with the PCA, the data are normalized if the option is activated. Normalization is done by subtracting the mean and dividing it by the standard deviation of each property.

Data points containing any properties with no-data value are excluded from the PCA.

Warning

If all points contain one no-data value, PCA cannot be performed. There should be at least as many valid data points (no empty data) as there are properties.

Interface

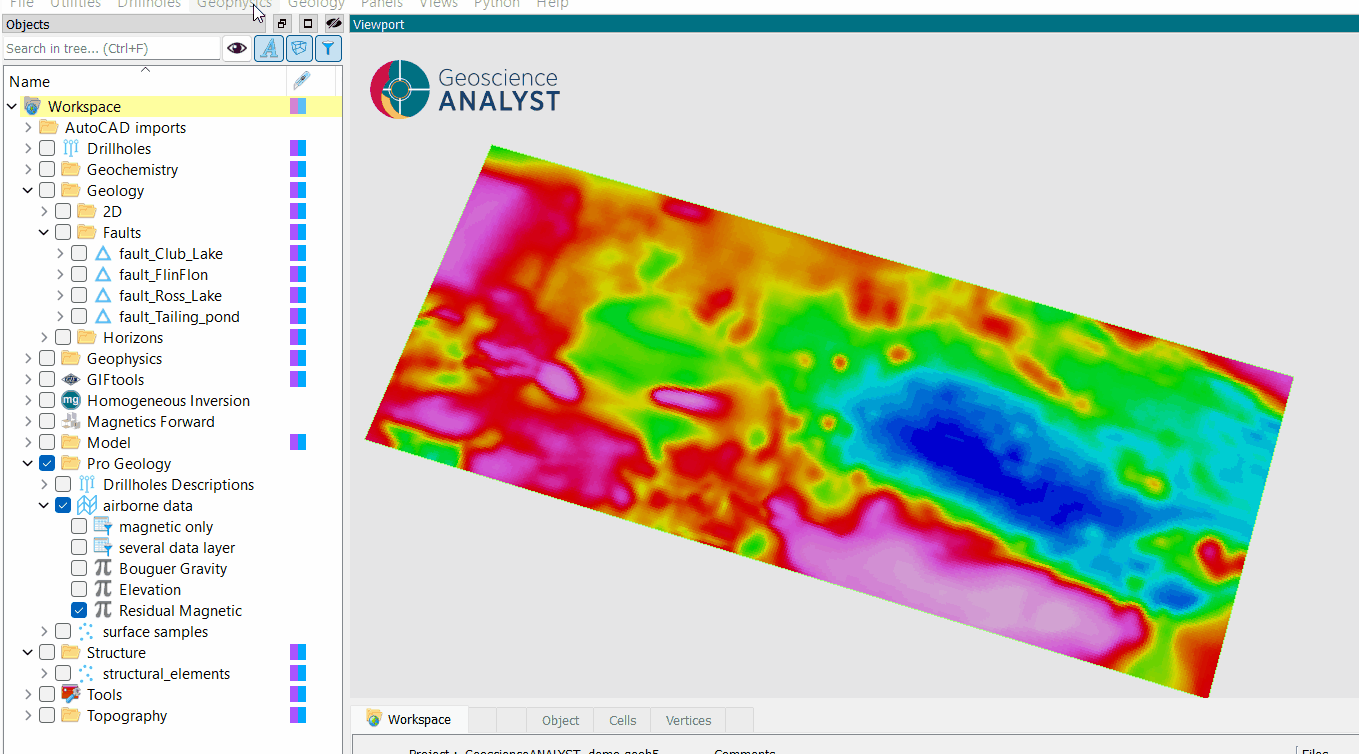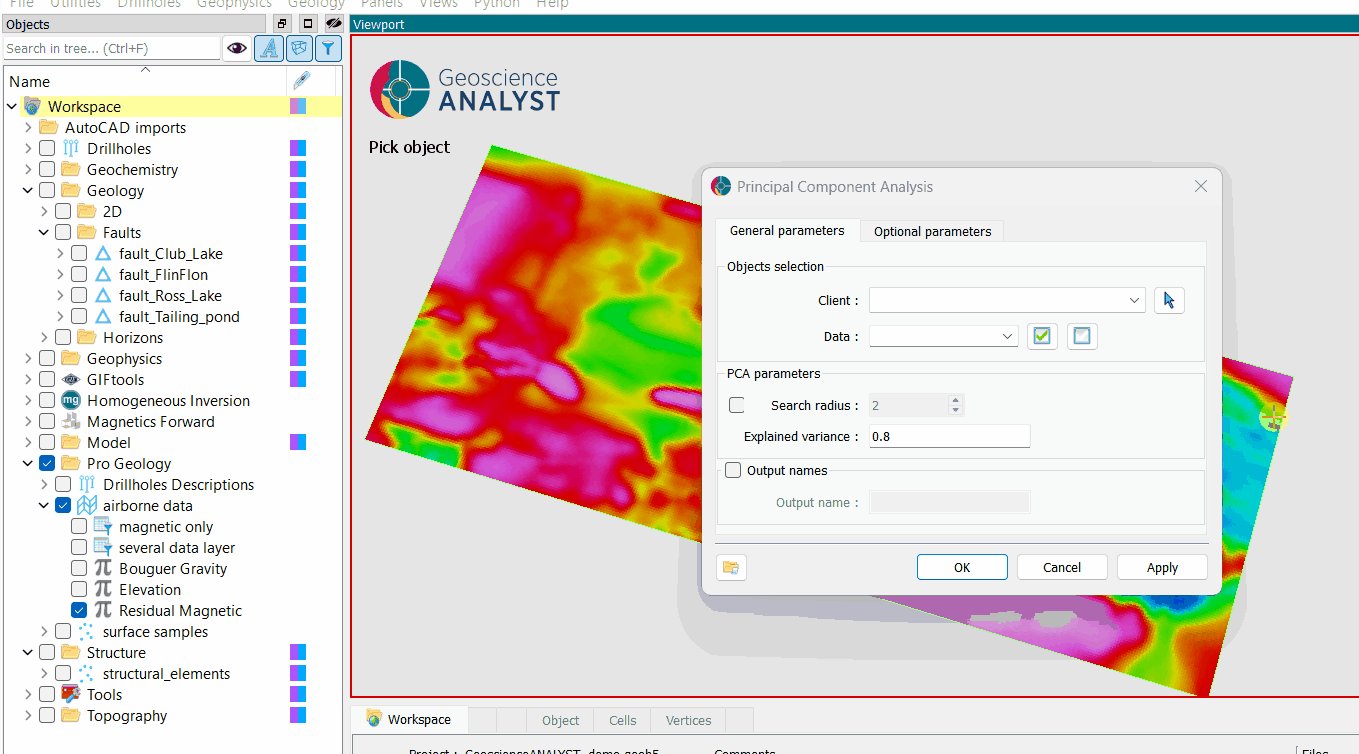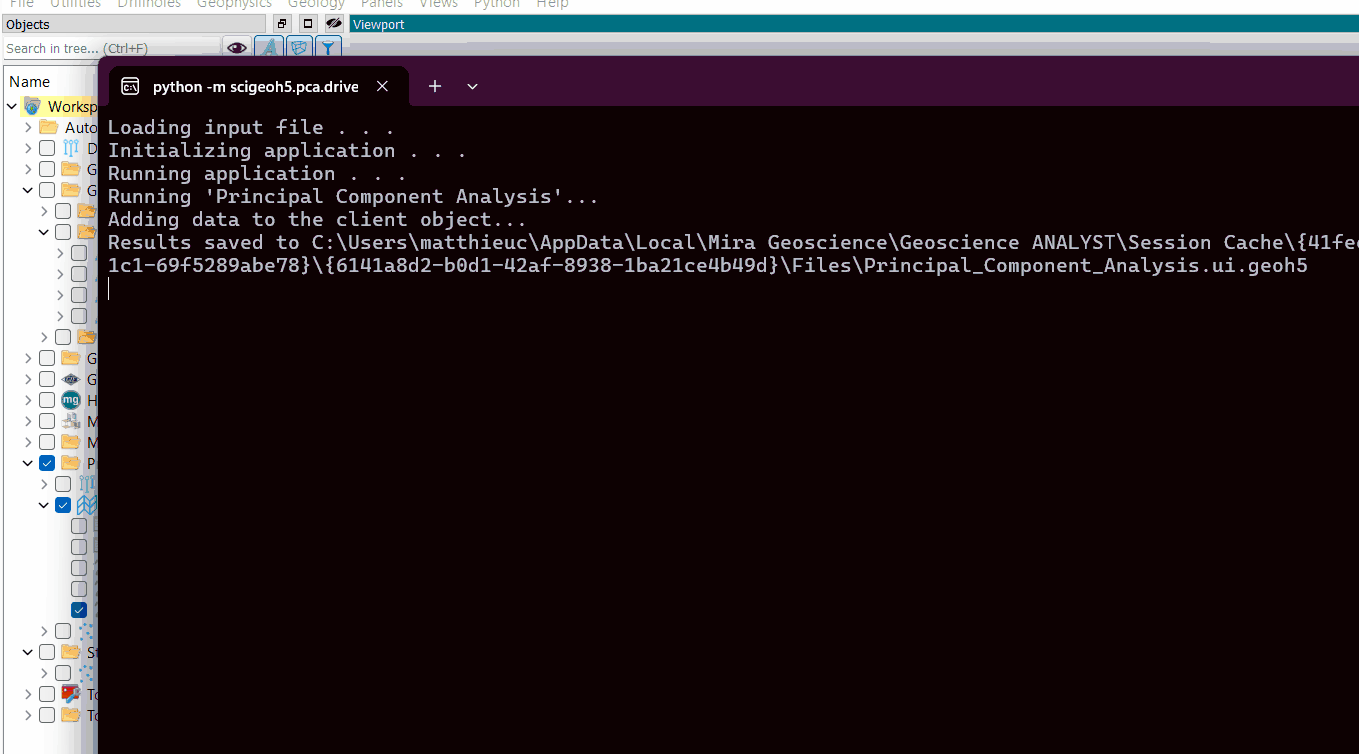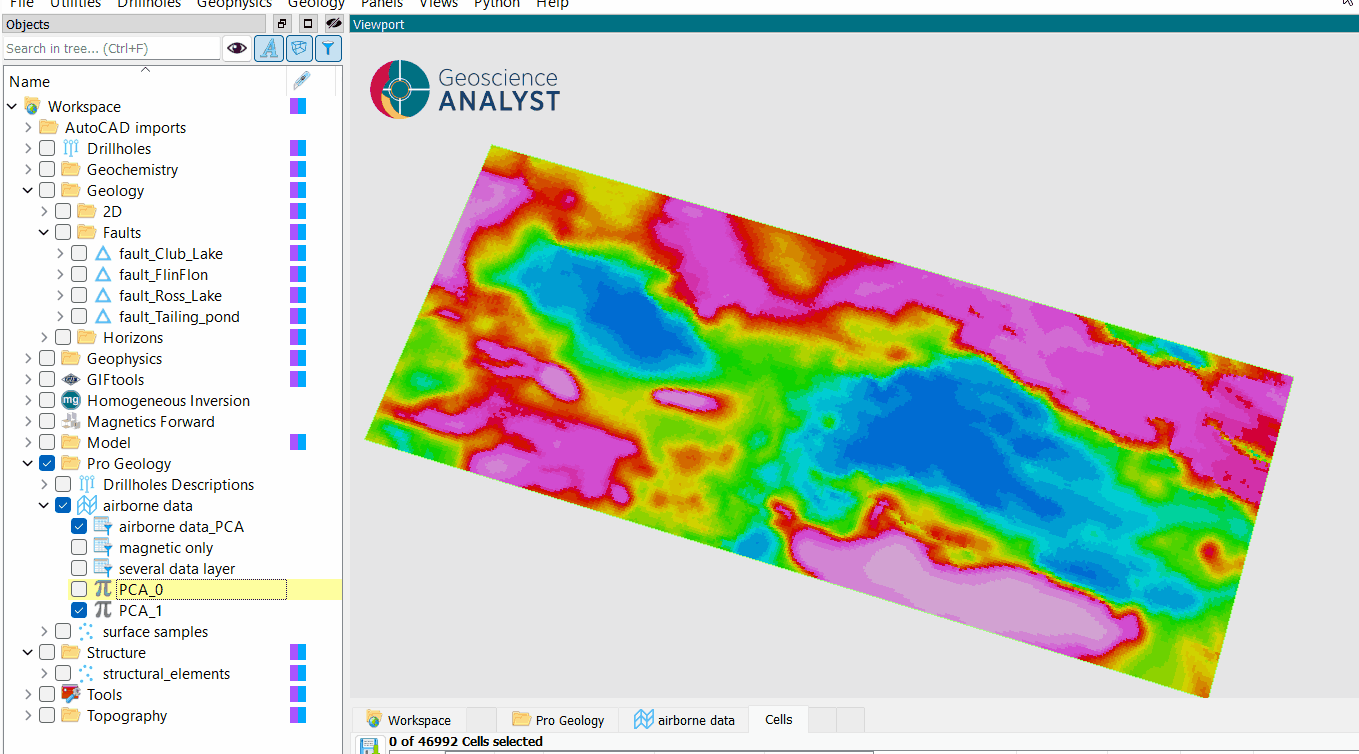
The general parameters controlling the Principal Component Analysis are shown in the figure below.

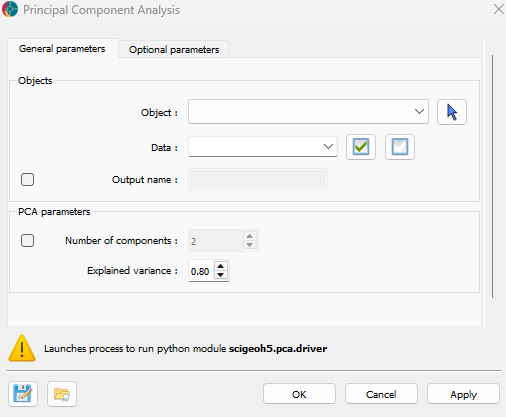
The options are described as follows:

• Object: The object containing the data to be analyzed.

• Data: The data to be analyzed. Users can select as many Float data properties as desired.

• Output name (optional): The name of the output group. If not specified, the output will default to the input data name appended with “PCA”.

• Number of components (optional): The number of principal components to compute. Must be an integer greater than 0.

• Explained variance (default = 0.8): The total variance to be explained by the principal components. This must be a float between 0 and 1, representing the percentage of total variance. This option is used only if Number of components is not set.

Optional Parameters

Advanced controls on the Scikit-Learn PCA algorithm are available as optional parameters, as shown in the figure below.

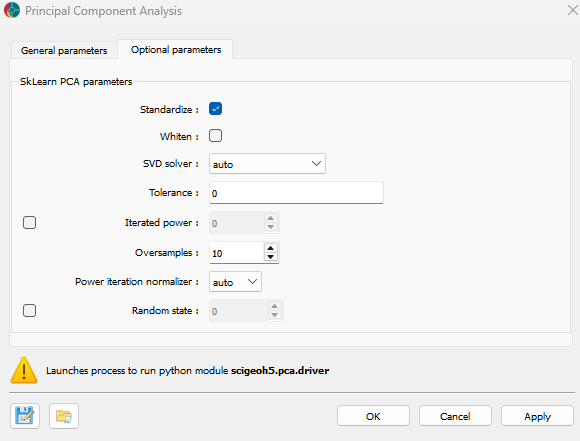
• Standardize (optional): If checked, the data will be normalized before performing Principal Component Analysis (PCA).

• Whiten (optional): If checked, the components are scaled to unit variance. Whitening removes correlations between features but may reduce interpretability.

• SVD solver (default=’auto’): Determines the algorithm used for computing the principal components. Options include:

  • auto: Chooses the solver based on data size.

  • full: Uses a full Singular Value Decomposition (SVD) approach.

  • arpack: Uses a truncated SVD.

  • randomized: Uses a fast, approximate randomized SVD.

• Tolerance (default=0.0): The tolerance for the singular values computed during the SVD.

• Iterated power (optional, default=0): The number of iterations for the randomized SVD solver.

• Oversamples (default=10): The number of additional random vectors to sample the range of the matrix.

• Power iteration normalizer (default=’auto’): The method to normalize the power iterations. Options include:

  • auto: Chooses the normalizer based on the solver.

  • QR: Uses the QR decomposition (a mathematical decomposition method for matrices).

  • LU: Uses the LU decomposition (another method for matrix factorization).

• random_state (optional): Controls the randomness of the solver when svd_solver = randomized. Pass an integer for reproducibility.

Once the parameters are selected, press OK to run the analysis.

Results

The application create a new group, as presented in the figure below. This group is named as defined in the Output name parameter and the new data created are name PCA_n where n is the number of the component.

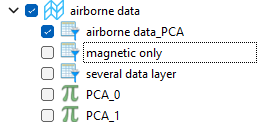
Tutorial

The following video presents a tutorial on how to use the PCA application.

• Opening the application.

• Selecting the Object containing the data.

• Selecting the data to be analyzed.

• Run the application.

• Inspect the computed principal components.